6. Unterrichtsblock

Kursinhalte

Python Grundlagen
Perzeptron Lernregel

Wiederholung: Python-Grundlagen

Folgende Konzepte kennst du schon aus dem Python Unterricht. Hier kommt eine kurze Wiederholung, da sie wichtig sind für die weitere Unterrichtsreihe.

Funktionen: Funktionen helfen uns, Code zu strukturieren und wiederzuverwenden. Sie werden nur dann ausgeführt, wenn sie aufgerufen werden.
Mehr zu Funktionen findest du im Python-Entwicklerkurs: https://pythonentwicklerkurs.de/1-2-semester/9-unterrichtsblock/

def kugel_volumen(radius, kommastellen):
    pi = 3.14159
    volumen = (4 / 3) * pi * radius ** 3
    volumen = round(volumen, kommastellen)
    return pi, radius, volumen

pi, radius, volumen = kugel_volumen(5, 3)

print("Eine Kugel mit dem Radius " + str(radius) + 
      " hat das Volumen " + str(volumen) + 
      "\nIn der Formel benutzt man pi = " + str(pi))

Booleans: Wahrheitswerte steuern Entscheidungen im Code.
Mehr zu Booleans findest du im Python-Entwicklerkurs: https://pythonentwicklerkurs.de/1-2-semester/4-unterrichtsblock/

bild_ist_hund = True

if bild_ist_hund:
    print("Das Bild zeigt einen Hund.")
else:
    print("Kein Hund erkannt.")

if-Statements: Entscheidungen treffen – je nach Bedingung.
Mehr zu if-Statements findest du im Python-Entwicklerkurs: https://pythonentwicklerkurs.de/1-2-semester/8-unterrichtsblock/

bild_klasse = "Katze"

if bild_klasse == "Hund":
    print("Das Bild zeigt einen Hund.")
elif bild_klasse == "Katze":
    print("Das Bild zeigt eine Katze.")
else:
    print("Unbekanntes Tier erkannt.")

for-Schleifen: Wiederholungen über Listen oder Bereiche.
Mehr zu for-Schleifen findest du im Python-Entwicklerkurs: https://pythonentwicklerkurs.de/1-2-semester/8-unterrichtsblock/

for i in range(5):
    print(i)

while-Schleifen: Wiederholen, solange eine Bedingung erfüllt ist.
Mehr zu while-Schleifen findest du im Python-Entwicklerkurs: https://pythonentwicklerkurs.de/1-2-semester/8-unterrichtsblock/

zähler = 0
while zähler < 3:
    print("Durchlauf", zähler)
    zähler += 1

Klassen definieren: Objekte und Strukturen bauen – wichtig für das Perzeptron.
Mehr zu Klassen findest du im Python-Entwicklerkurs: https://pythonentwicklerkurs.de/1-2-semester/11-unterrichtsblock/

class Neuron:
    def __init__(self, gewicht):
        self.gewicht = gewicht

Machine Learning Algorithmus

Mit Hilfe von Machine Learning lernen wir die passenden Gewichte mithilfe der Perzeptron-Lernregel. Diese Regel dient dazu, die Gewichte W so anzupassen, dass eine Trennlinie (bzw. Trennebene) in die Trainingsdaten gelegt wird – sodass eine Klasse oberhalb und die andere unterhalb dieser Grenze liegt.

Gewichte sind Zahlen, die bestimmen, wie stark einzelne Eingabewerte das Ergebnis beeinflussen. Sie werden mit den Eingaben multipliziert und entscheiden, ob das Perzeptron „aktiviert“ wird – also ob es z. B. einen Hund erkennt oder nicht. Durch das Lernen verändern sich die Gewichte so, dass die Entscheidung immer besser wird.

Trennlinie einzeichnen

Funktion zur Visualisierung eines Perzeptron-Modells

# Funktion zur Visualisierung eines Perzeptron-Modells
import matplotlib.pyplot as plt
def visualize(features, labels, w):         # features: Trainingsdaten, labels: Farbcodierung, w: Linie
    plt.title('Trainingsdaten')
    plt.xlabel('Grösse [cm]')
    plt.ylabel('Länge [cm]')
    plt.scatter(features[:, 0], features[:, 1], c=labels)      #c: color

Wenn wir die Funktion ausführen bekommen wir diesen Plot:

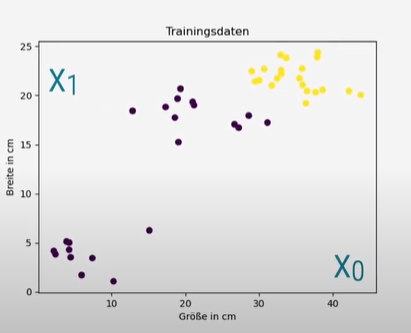
Jetzt fehlt noch die Trennlinie. Die Linie ist definiert durch w*x > 0. Wobei w*x das Skalarprodukt der Vektoren w und x ist. Nun muss die Ungleichung umgeschrieben werden:

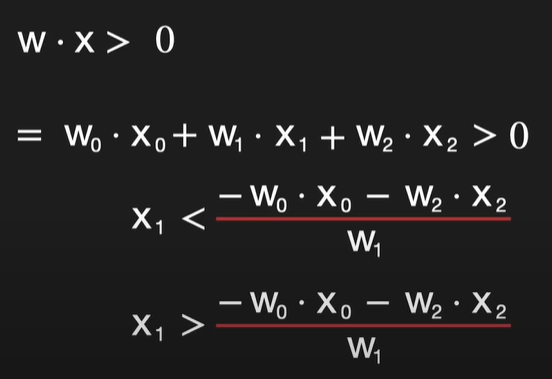
Wenn jetzt W₁ positiv ist und das Symbol ein größer ist, ist die Klasse Hund über der Linie.

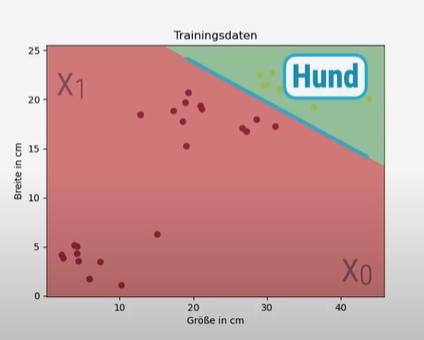
Wenn jetzt W₁ negativ ist und das Symbol beim Umschreiben zu kleiner wird, ist die Klasse Hund unter der Linie.

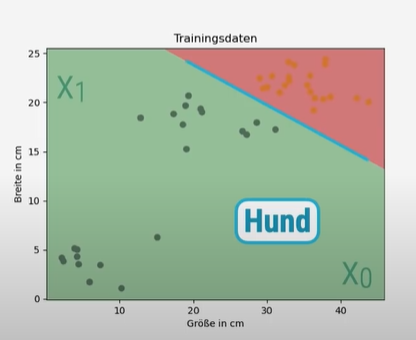
Nun fügen wir die Trennlinie ein und erhalten folgenden Plot:

if w[1] != 0:
    x0 = np.array([min(feature[:, 0]), max(feature[:, 0])])
    x1 = -(w[0] * x0 + w[2]) / w[1]
    plt.plot(x0, x1)

plt.show()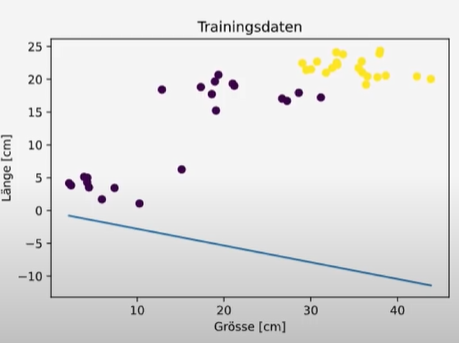

Perzeptron-Lernregel

Damit die Trennlinie an der richtigen Stelle liegt, brauchen wir passende Gewichte – diese lernen wir mithilfe der Perzeptron-Lernregel.

Was ist die Perzeptron-Lernregel?

Die Perzeptron-Lernregel ist ein Algorithmus der zum Supervised Learning gehört.

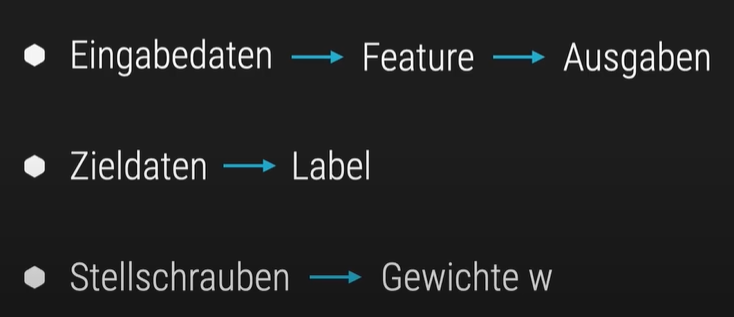
Label und Aufgaben vergleichen

Hinweis: Die Kombinationen aus ausgabe und label ergeben vier mögliche binäre Paare:

00 und 11 bedeuten, dass das Perzeptron korrekt klassifiziert hat (Ausgabe stimmt mit dem Label überein).
01 steht für einen falsch-negativen Fall: Das Modell sagt „Nein“, obwohl die richtige Antwort „Ja“ gewesen wäre.
10 steht für einen falsch-positiven Fall: Das Modell sagt „Ja“, obwohl die richtige Antwort „Nein“ gewesen wäre.

x = feature[0]
label = labels[0]
ausgabe = perzeptron(w, x)

if ausgabe == label:
    pass  # 1. 00 oder 11 → korrekt klassifiziert
elif ausgabe == 0 and label == 1:
    pass  # 2. 01 → falsch negativ
elif ausgabe == 1 and label == 0:
    pass  # 3. 10 → falsch positiv
# 4. 11 → bereits im ersten Fall abgedeckt

Gewichte anpassen

Im Vergleich zum vorherigen Code, der nur die Fälle prüft und mit pass darauf reagiert, kommt hier Lernlogik hinzu: Das Perzeptron passt seine Gewichtungen an, wenn es falsch liegt.

Fall 2 (ausgabe = 0, label = 1): Das Modell hat „Nein“ gesagt, obwohl die richtige Antwort „Ja“ gewesen wäre → Fehler. → Lösung: Die Eingabe x wird zu den Gewichten w hinzuaddiert, um die Entscheidung in Zukunft zu korrigieren.
Fall 3 (ausgabe = 1, label = 0): Das Modell hat „Ja“ gesagt, obwohl die richtige Antwort „Nein“ gewesen wäre → Fehler. → Lösung: Die Eingabe x wird von den Gewichten w abgezogen, um die Entscheidung in Zukunft zu korrigieren.

Diese Gewichtsanpassung ist das zentrale Lernprinzip des Perzeptrons: Es verändert sich durch Fehler – und wird dadurch besser in der Klassifikation.

x = feature[0]
label = labels[0]
ausgabe = perzeptron(w, x)

if ausgabe == label:
    pass  # Fall 1 (00) oder Fall 4 (11): korrekt klassifiziert → keine Änderung
elif ausgabe == 0 and label == 1:
    w += x  # Fall 2 (01): falsch negativ → Gewichte verstärken
elif ausgabe == 1 and label == 0:
    w -= x  # Fall 3 (10): falsch positiv → Gewichte abschwächen

oder kürzer:

delta = label - perzeptron(w, x)
w += delta * x

Dieser Code ist eine kompakte Version des Lernalgorithmus für ein Perzeptron. Er kombiniert die Fehlerberechnung und die Gewichtsanpassung in nur zwei Zeilen:

Fehler berechnen:delta = label - perzeptron(w, x) → Vergleicht die tatsächliche Zielausgabe (label) mit der vom Perzeptron berechneten Ausgabe. → Ergebnis:
- delta = 0 → korrekt klassifiziert
- delta = +1 → falsch negativ (Modell hat 0 gesagt, obwohl 1 richtig wäre)
- delta = -1 → falsch positiv (Modell hat 1 gesagt, obwohl 0 richtig wäre)
Gewichte anpassen: w += delta * x → Wenn delta = 0, passiert nichts. → Wenn delta = +1, wird x zu w addiert → Verstärkung → Wenn delta = -1, wird x von w subtrahiert → Abschwächung

Wie wurde der Code gekürzt?

Im vorherigen Beispiel war die Lernlogik in drei Bedingungen aufgeteilt:

python

if ausgabe == label:
    pass
elif ausgabe == 0 and label == 1:
    w += x
elif ausgabe == 1 and label == 0:
    w -= x

Die kompakte Version ersetzt diese drei Fälle durch eine mathematische Formel:

Sie nutzt die Tatsache, dass label - ausgabe direkt den Lernimpuls ergibt:
- 0 → kein Fehler
- +1 → Verstärken
- –1 → Abschwächen

Dadurch wird der Code kürzer, eleganter und leichter skalierbar, z. B. für Vektoren oder Batch-Verarbeitung.

Der bisherige Code zeigt, wie das Perzeptron eine einzelne Eingabe klassifiziert – also ob z. B. ein Tier als „Hund“ erkannt wird oder nicht. Das ist ein wichtiger Schritt, aber: Ein einzelnes Beispiel reicht nicht aus, damit das Modell wirklich lernt.

Damit das Perzeptron die richtige Trennlinie findet, muss es alle Trainingsdaten durchlaufen – also jedes Tier einzeln prüfen. Und bei jedem Fehler muss es die Gewichte anpassen, damit die Entscheidung beim nächsten Mal besser wird.

Das bedeutet:

Wir brauchen eine Schleife, die alle Datenpunkte durchgeht
Bei jedem Durchlauf wird geprüft, ob die Klassifikation stimmt
Wenn nicht, werden die Gewichte verändert – das ist die eigentliche Lernregel

Erst wenn wir diesen Lernprozess eingebaut haben, kann das Perzeptron wirklich lernen, zwischen „Hund“ und „kein Hund“ zu unterscheiden. Der aktuelle Code ist also nur der Anfang – das Lernen fehlt noch.

Einbauen der For-Schleife

Als erstes müssen wir uns überlegen über welche Daten wir iterieren. Die benötigten Variablen sind w, x und Label.

Wir wollen die Lernregel über alle Label und alle Feature durchrechnen, also müssen wir über 2 Listen iterieren.

# Schleife über alle Trainingsdaten
for index in range(len(feature)):
    
    # Eingabevektor und zugehöriges Label holen
    x = feature[index]
    label = labels[index]
    
    # Ausgabe des Perzeptrons berechnen und Fehler bestimmen
    delta = label - perzeptron(w, x)
    
    # Gewichte anpassen: 
    # - Wenn delta = 0 → keine Änderung (korrekt klassifiziert)
    # - Wenn delta = +1 → Eingabe x zu w addieren (falsch negativ)
    # - Wenn delta = –1 → Eingabe x von w subtrahieren (falsch positiv)
    w += delta * x

Dieser Code zeigt den vollständigen Lernschritt: Das Modell geht alle Trainingsbeispiele durch, prüft die Klassifikation und passt die Gewichtung an, wenn es falsch liegt. So „lernt“ das Perzeptron, die Trennlinie zwischen Klassen zu verbessern.

oder:

# Schleife über alle Trainingsdaten (Feature-Vektor und zugehöriges Label)
for x, label in zip(feature, labels):
    
    # Berechnung des Fehlers: Differenz zwischen tatsächlichem Label und Modell-Ausgabe
    delta = label - perzeptron(w, x)
    
    # Gewichtsanpassung: 
    # - Wenn delta = 0 → keine Änderung (korrekt klassifiziert)
    # - Wenn delta = +1 → Eingabe x zu w addieren (falsch negativ)
    # - Wenn delta = –1 → Eingabe x von w subtrahieren (falsch positiv)
    w += delta * x
    
    # Fehlerzähler erhöhen, wenn eine Fehlklassifikation vorliegt
    if delta != 0:
        fehler += 1

Hinweis:

Die kompakte Schreibweise mit zip() macht den Code kürzer und besser lesbar, da Eingaben und Labels direkt als Paare verarbeitet werden – ganz ohne Indexverwaltung. Der Lernschritt wird klar strukturiert: Fehler werden berechnet, Gewichte angepasst und Fehlklassifikationen gezählt. So entsteht ein eleganter, praxisnaher Code, der sich ideal für den Einstieg ins maschinelle Lernen mit dem Perzeptron eignet.

Nachdem der Code mit einer For-Schleife ausgeführt wurde, zeigt die Visualisierung, dass die Trennlinie immer noch weit von der optimalen Lösung entfernt ist. Eine genauere Analyse offenbart:

Nur ein Datenpunkt falsch klassifiziert: Zuerst wurden alle „Hunde“-Daten korrekt klassifiziert. Beim ersten „Nicht-Hund“-Datenpunkt wurde ein Fehler gemacht, woraufhin die Gewichte angepasst wurden.
Seitenwechsel: Die Anpassung der Gewichte führte dazu, dass die Klassen die Seiten der Trennlinie wechselten, sodass nun alle Datenpunkte als „Nicht-Hund“ klassifiziert wurden.
Das Problem: Eine einmalige Iteration über den Datensatz (eine Epoche genannt) reicht nicht aus, um die optimale Trennlinie zu finden.

Die Lösung: Man muss die For-Schleife (also eine Epoche) mehrmals wiederholen (z.B. 10, 20 oder 100 Mal), bis die Perzeptron-Lernregel die richtige Linie findet. Dies wird Thema des nächsten Videos sein, das die Verwendung von While-Schleifen zur Steuerung der Epochenanzahl einführen wird.

Einbauen der While-Schleifen

Die zuvor entwickelte For-Schleife, die eine einzelne Trainings-Epoche abbildet, wird nun in eine While-Schleife eingebettet. Dadurch lässt sich das Perzeptron über mehrere Epochen hinweg trainieren – solange Fehler auftreten und eine maximale Epochenzahl (z. B. 100) nicht überschritten wird.

Lernbedingung

Die While-Schleife läuft unter zwei Bedingungen:

Es sind noch Klassifizierungsfehler vorhanden (fehler != 0)
Die maximale Anzahl an Epochen wurde noch nicht erreicht

Fehlerüberwachung

Vor jeder Epoche wird die Fehleranzahl auf null gesetzt. Innerhalb der For-Schleife wird sie bei jeder falschen Klassifizierung erhöht. So lässt sich die Lernfortschritt gezielt überwachen.

Vorzeitiges Beenden

Sobald keine Fehler mehr auftreten, wird die Schleife mit break beendet. Das spart Rechenzeit und zeigt, dass das Modell eine fehlerfreie Trennung gefunden hat.

while iter < max_epochs:
    for x, label in zip(feature, labels):
        delta = label - perceptron(w, x)
        w += delta * x

        if delta != 0:
            fehler[iter] += 1

    if fehler[iter] == 0:
        visualize(feature, labels, w)
        break
    
    iter += 1

else:
    print("Es wurde keine Lösung gefunden.")

Anmerkung zur ELSE-Klausel:

Die else nach der while-Schleife wird ausgeführt, wenn die Schleife normal durchläuft, d.h., wenn sie nicht durch break verlassen wird. Im Kontext dieses Codes bedeutet das, dass das break nicht ausgelöst wurde (weil fehler[iter] == 0 nie erreicht wurde) und iter bis max_epochs hochgezählt wurde – also wurde keine Lösung gefunden. Das ist die korrekte logische Verwendung der else-Klausel bei while-Schleifen in Python.

Problem: Langsame Konvergenz

Auch nach 100 Epochen kann es vorkommen, dass das Perzeptron keine Lösung findet. In einem Beispiel dauert es über 9.000 Epochen, bis die Fehlerrate auf null sinkt – ein Hinweis auf ineffizientes Lernen.

Lösung: Normalisierung der Trainingsdaten

Die Eingabedaten werden so skaliert, dass sie in einen definierten Wertebereich fallen – z. B. zwischen 0 und 1. Dadurch wird das Lernverhalten stabiler und schneller.

Die Maximalwerte der einzelnen Features werden ermittelt, und alle Werte durch diese Maxima geteilt. So entsteht ein gleichmäßiger Wertebereich für alle Eingaben.

Nach der Normalisierung sinkt die Anzahl der benötigten Epochen drastisch – von über 9.000 auf nur drei. Ein eindrucksvolles Beispiel für die Bedeutung von „Best Practices“ im Machine Learning.

maximum = np.max(feature, 0)
skalierungsfaktor = np.max(feature, 0)
feature /= skalierungsfaktor

Jetzt sollte die Trennlinie richtig angezeigt werden.

Nun sollte der bisherige Code so aussehen:

import numpy as np
import matplotlib.pyplot as plt

# --- 1. Funktion: Perzeptron-Ausgabe ---
def perzeptron(w, x):
    return int(np.dot(w, x) >= 0)  # Schwellenwert bei 0

# --- 2. Visualisierung ---
def visualize(features, labels, w):
    plt.scatter(features[:, 0], features[:, 1], c=labels)
    
    # Trennlinie berechnen (nur bei 2D-Daten mit Bias-Term w[2])
    if w[1] != 0:
        x0 = np.array([min(features[:, 0]), max(features[:, 0])])
        x1 = -(w[0] * x0 + w[2]) / w[1]
        plt.plot(x0, x1)
    
    plt.title("Perzeptron-Trennung")
    plt.show()

# --- 3. Trainingsdaten vorbereiten ---
# Beispielhafte Daten (2D + Bias-Term)
features = np.array([
    [2, 3, 1],   # letzter Wert = Bias-Eintrag
    [1, 1, 1],
    [4, 5, 1],
    [0, 0, 1]
])
labels = np.array([1, 0, 1, 0])

# --- 4. Normalisierung der Merkmale (ohne Bias-Spalte) ---
skalierungsfaktor = np.max(features[:, :2], axis=0)
features[:, :2] /= skalierungsfaktor

# --- 5. Initialisierung ---
w = np.zeros(3)         # Gewichtungsvektor inkl. Bias
max_epochs = 20         # maximale Anzahl Durchläufe
fehler = []             # Fehlerliste pro Epoche
iter = 0                # Startwert für Epoche

# --- 6. Lernschleife über mehrere Epochen ---
while iter < max_epochs:
    fehler.append(0)  # Fehlerzähler für aktuelle Epoche

    for x, label in zip(features, labels):
        delta = label - perzeptron(w, x)
        w += delta * x

        if delta != 0:
            fehler[iter] += 1

    if fehler[iter] == 0:
        print(f"Modell hat in Epoche {iter} korrekt klassifiziert.")
        visualize(features, labels, w)
        break

    iter += 1

else:
    print("Es wurde keine Lösung gefunden.")

Video:
#14: https://www.youtube.com/watch?v=DXpk5hniOK4&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=14
#15: https://www.youtube.com/watch?v=-U9mQl4R2WA&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=15
#16: https://www.youtube.com/watch?v=Gg4-KNG76KI&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=17
#17: https://www.youtube.com/watch?v=GFUz1bENOUM&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=17 #18: https://www.youtube.com/watch?v=5xSbiRHUnZc&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=18
#19: https://www.youtube.com/watch?v=F84-PKteV4A&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=19