5. Unterrichtsblock

KI Entwicklerkurs

Kursinhalte

  • Funktion Y des Perzeptrons
  • Das Skalarprodukt
  • Der Bias
  • Daten vorbereiten
  • Gewichte initialisieren

Funktion Y des Perzeptrons

Einleitung

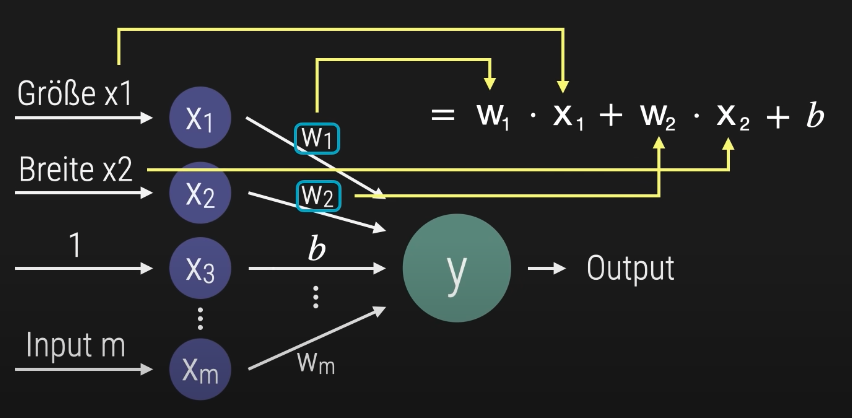
Die Funktion eines Perzeptrons basiert auf einer gewichteten Summe der Eingabesignale. Jeder Input – etwa Größe, Breite oder weitere Merkmale – wird mit einem zugehörigen Gewicht multipliziert. Anschließend wird ein Bias-Wert addiert, um die Entscheidungsschwelle zu verschieben.

Die dargestellte Struktur zeigt, wie mehrere Eingabewerte über ihre jeweiligen Gewichtungen zu einem Gesamtwert verrechnet werden. Dieser Wert bildet die Grundlage für die Klassifikationsentscheidung des Perzeptrons.

Diese Berechnung lässt sich effizient mit vektorisierten Operationen in Python umsetzen – insbesondere mit NumPy.

Ziel ist es, die logische Struktur hinter der Perzeptron-Funktion zu verstehen und ihre Umsetzung im Code nachvollziehen zu können.

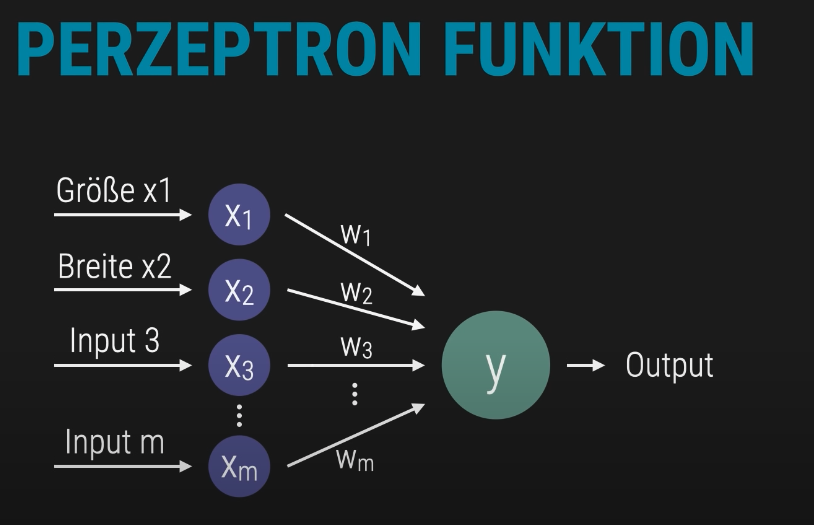
Mathematische Darstellung der Funktion Y

Die Kernfunktion des Perzeptrons lässt sich durch die Gleichung Y = w ⋅ x + b beschreiben. Dabei stehen die Gewichte (w) für die Stärke der Verbindungen, die Eingangssignale (x) für die Features und der Bias (b) für eine Verschiebung des Entscheidungswertes. Diese Berechnung ist eine elementare Operation in neuronalen Netzen und bildet die Grundlage für die Klassifikationsentscheidung.

Im Folgenden wird erläutert, wie diese Funktion Schritt für Schritt verstanden und effizient in Python umgesetzt werden kann – insbesondere mithilfe von NumPy, das vektorisierte Operationen ermöglicht und die Berechnung deutlich beschleunigt. Ziel ist es, die Funktionsweise der Y-Gleichung klar nachzuvollziehen und ihre praktische Anwendung im Code zu verstehen.

Gesamte Funktion Y
Heutiger Teil der Programmierung

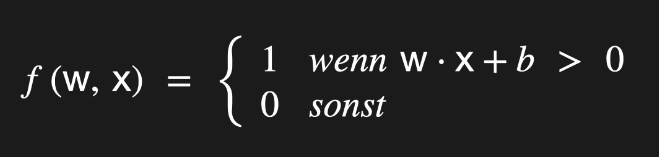
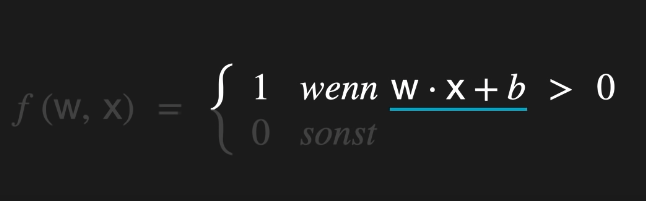
Das Skalarprodukt

In einem Perzeptron liegen die Gewichte und Eingangssignale in der Regel als Vektoren vor – bezeichnet als w⃗\vec{w} für die Gewichte und x⃗\vec{x} für die Eingabefeatures. Die zentrale Rechenoperation zwischen diesen beiden Vektoren ist das Skalarprodukt.

Mathematische Definition

Das Skalarprodukt zweier gleich langer Vektoren wird berechnet, indem man die jeweils korrespondierenden Elemente miteinander multipliziert und die Produkte anschließend aufsummiert.

Für zwei Vektoren

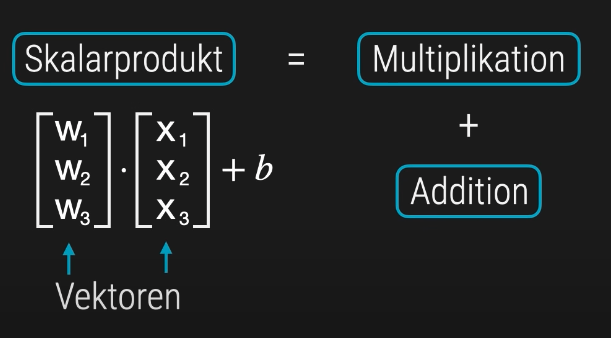
Skalarprodukte sind hintereinander aufsummierte Multiplikationen einzelner Vektoren.

ergibt sich das Skalarprodukt zu

Skalarprodukt ausgeschrieben

Intuitive Bedeutung

Das Skalarprodukt entspricht einer gewichteten Summe der Eingangssignale. Jedes Feature trägt entsprechend seines zugeordneten Gewichts zur Gesamtsumme bei. Diese Summe bildet die Grundlage für die Aktivierung des Perzeptrons und entscheidet darüber, ob eine Klassifikation ausgelöst wird.

Der Bias (Voreingenommenheit)

Der Bias ist ein fester Bestandteil der Perzeptron-Funktion und wird im Deutschen häufig als „Voreingenommenheit“ bezeichnet. Er stellt einen konstanten Wert dar, der zur gewichteten Summe der Eingabesignale addiert wird.

Zweck des Bias

Der Bias ermöglicht es, die durch das Perzeptron definierte Entscheidungsgrenze – also die Trennlinie oder Hyperebene – im Merkmalsraum zu verschieben. Ohne Bias würde diese Grenze immer durch den Ursprung verlaufen, was die Modellierungsmöglichkeiten stark einschränken würde.

Modellierung durch Dimensions-Erweiterung

Um den Bias mathematisch elegant in die Berechnung zu integrieren, wird häufig ein zusätzlicher Eingabewert x3x_3 eingeführt, der konstant den Wert 1 hat. Der Bias bb wird dann als Gewicht w3w_3 dieses künstlichen Eingangs behandelt.

Die ursprüngliche Formel

Y = w1⋅x1+w2⋅x2+b

wird dadurch umformuliert zu

Y = w1⋅x1+w2⋅x2+w3⋅x3 mit x3 = 1 und w3=b

Zusätzliches Hinzufügen eines „Bias“, falls mehrere Werte „0“ sind
Survivorship Bias
Der Bias wird in die Eingangssignale eingefügt
Wenn wir b bereits als Gewichtsvektor verwenden, vereinfacht sich die gesamte Formel

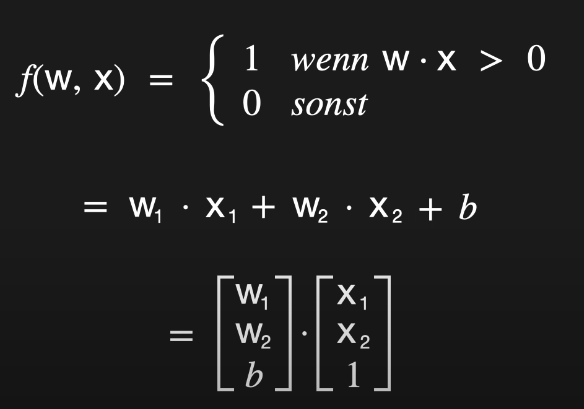
Vorteil

Diese Umformulierung erlaubt eine einheitliche, vektorisierte Berechnung aller Komponenten – inklusive des Bias – und vereinfacht die Implementierung in Python, insbesondere mit NumPy.

Datenvorbereitung für das Perzeptron: Bias integrieren

Bevor ein Perzeptron Eingabedaten verarbeiten kann, müssen diese in eine geeignete Form gebracht werden. Ein zentraler Schritt dabei ist die Erweiterung des Eingabevektors um den Bias-Term.

In der gezeigten Struktur besteht der ursprüngliche Eingabevektor aus numerischen Merkmalen wie Größe und Breite. Diese Merkmale werden aus einem NumPy-Array extrahiert, z. B. durch x = feature[0, 1:], wobei die erste Spalte (z. B. eine ID oder Klassenbezeichnung) übersprungen wird.

Um den Bias mathematisch konsistent in die Berechnung einzubinden, wird ein zusätzlicher Wert 1 an das Ende des Vektors eingefügt. Dies geschieht mit der Funktion np.insert(x, 2, 1). Der Bias wird anschließend als zusätzliches Gewicht behandelt, das mit diesem konstanten Eingang multipliziert wird.

Die resultierende Berechnung folgt der erweiterten Formel:

Y=w1⋅x1+w2⋅x2+bwird zuY=w1⋅x1+w2⋅x2+w3⋅x3mitx3=1,  w3=b

Diese Technik erlaubt eine einheitliche, vektorisierte Berechnung aller Eingaben inklusive Bias und ist besonders effizient in NumPy-basierten Implementierungen.

Über die insert() Funktion können wir den Bias mit dem Wert 1 zu unseren Eingangswerten hinzufügen

Gewichte initialisieren: Zwei Ansätze im Vergleich

Die Gewichte wurden in den vorherigen Unterrichtsstunden auch als „Wiederstände“ bezeichnet

Bevor ein Perzeptron mit dem Training beginnen kann, müssen die Gewichte initialisiert werden. Diese bestimmen, wie stark jedes Eingangssignal zur Gesamtentscheidung beiträgt. Die Grafik zeigt zwei typische Ansätze:

Ansatz A: Gewichte als Nullen

w = np.zeros(3)
  • Alle Gewichte starten bei 0.
  • Die Berechnung ergibt zunächst:

Y=0⋅x1+0⋅x2+0

  • Vorteil: Einfach und kontrolliert.
  • Nachteil: Kann zu langsamer Konvergenz führen, da alle Neuronen gleich starten.

Ansatz B: Zufällige Initialisierung

w = np.random.rand(3)

Die Gewichte werden mit Zufallswerten zwischen 0 und 1 belegt.

Vorteil: Bringt Variation ins Modell und kann das Lernen beschleunigen.

Nachteil: Ergebnisse sind nicht direkt reproduzierbar, es sei denn, ein Zufallsseed wird gesetzt

Daraus ergibt sich folgender Code:

import numpy as np

# --- 1. Vorbereitung der Eingabedaten (Features) ---

# Annahme: 'feature' ist ein geladenes NumPy-Array mit Trainingsdaten (z.B. feature[0] ist das erste Tier)

# Extrahieren der Merkmale (Größe und Breite) des ersten Datenpunkts
x = feature[0] 

# Hinzufügen des fiktiven Eingangssignals 1 für den Bias-Trick
# Dies erweitert den Eingabevektor x um den Wert 1 (z.B. [Größe, Breite] wird zu [Größe, Breite, 1])
x = np.insert(x, len(x), 1) 

# --- 2. Initialisierung der Gewichte ---

# Erstellung der Gewichte (w) als Zufallswerte
# Der Vektor w muss die gleiche Länge wie x haben (inkl. Bias-Gewicht)
w = np.random.rand(len(x)) 
# Alternativ: w = np.zeros(len(x))

# --- 3. Berechnung der Perzeptron-Kernfunktion (Y) ---

# Y = w ⋅ x + b
# Die NumPy-Funktion np.dot berechnet effizient das Skalarprodukt (die gewichtete Summe)
y = np.dot(w, x)

# Alternativ (Matrix-Multiplikation):
# y = x @ w

Aufgaben

Erstelle eine Funktion „eingangssignale“ welche den o. g. Code ausführt und als Argument Werte aus den Trainingsdaten enthalten kann.

Video:
#13: https://www.youtube.com/watch?v=k7rxRtMVskc&list=PLIYzsTnFhywyjBon1_tE4ZGVzXAx5FpWr&index=13